设事件A={使函数f（x）=ax²+x+b有两个相异零点}，

方程ax²+x+b=0有两个相异根，即△=1-4ab＞0，解得ab＜

1

4

，

∵在[1，4]上任取实数a，在[0，3]上任取实数b，

∴这是一个几何概型，所有的实验结果Ω={（a，b）|1≤a≤4且 0≤b≤3}；

事件A={（a，b）|ab＜

1

4

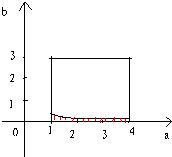
，1≤a≤4且 0≤b≤3}，在坐标系中画出图形：

则图中阴影部分是事件A构成的区域，则它的面积S=

∫

41

1

4a

da=

1

4

lna|₁⁴=

1

2

ln2，

∴事件A的概率P（A）=

1 2 ln2

9

=

ln2

18

．

故答案为：

ln2

18

．