搜题请搜索小程序“爱下问搜题”
问题 填空题
设f(x)=
x2-4x+6，x≥0
2x+4x＜0
若存在互异的三个实数x1，x2，x3，使f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围是______．
答案

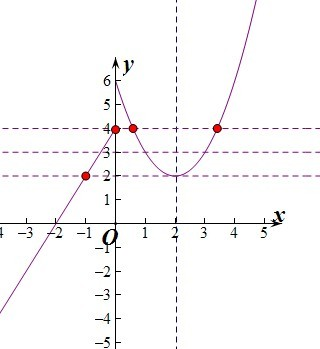
不妨设x1＜x2＜x3，当x≥0时f（x）=（x-2）2+2，

此时二次函数的对称轴为x=2，最小值为2，

作出函数f（x）的图象如图：

由2x+4=2得x=-1，由f（x）=（x-2）2+2=4时，解得x=2-

2
或x=2+
2
，

所以若f（x1）=f（x2）=f（x3），

则-1＜x1＜0，2-

2
＜x2＜2，2＜x3＜2+
2
，且
x2+x3
2
=2，即x2+x3=4，

所以x1+x2+x3=4+x1，

因为-1＜x1＜0，所以3＜4+x1＜4，

即x1+x2+x3的取值范围是（3，4）．

故答案为：（3，4）．

单项选择题 A1/A2型题

某患者骑跨伤后4天，排尿困难、 * * 口流血。查体：发热，阴囊明显肿大，发绀。其处理方法应是（）

A.立即以橡皮导尿管导尿并留置

B.立即以金属导尿管导尿

C.立即施行 * * 修补

D.立即行 * * 会师

E.耻骨上膀胱造瘘及引流外渗尿液
查看答案
完形填空

A guest comes up to Mrs. Dale, the Duty Manager, telling her 31        (anger) about the Hall Porter’s Department. Since there are 32        guests present, the Duty Manager invites the guest to come to her office 33         (talk) things over.

The guest says that the Hall Porter yesterday 34           (promise) to get theatre tickets 35          a show in the city. He says that today, 36            he went to collect the tickets there was  37          porter on duty. The porter could not find any tickets for the guest, and could not find any record of the request for       tickets. It seems that the porter on duty today did not believe 38                the guest had made any request for tickets. The guest says that the tickets were promised,   38                 he has planned to go to the theatre that night, and that it is the 40                (hotel) job to provide the tickets.
查看答案