∵对于任意的x∈R，都有f（x）•f（x+2）=10，∴f(x+4)=

10

f(x+2)

=f(x)

∴函数f（x）是一个周期函数，且T=4．

∵对x∈R都有f（-x）=f（x），

∴函数f（x）是定义在R上的偶函数，

∵当x∈[-2，0]时，f（x）=（

1

2

）^x-1，在区间（-2，6]内关于x的方程f（x）-log_a（x+2）=0恰有3个不同的实数解，

∴函数y=f（x）与y=log_a（x+2）在区间（-2，6]上有三个不同的交点，如下图所示：

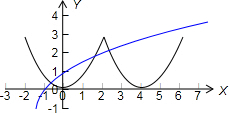
又f（-2）=f（2）=3，则有 log_a4＜3，且log_a8＞3，解得：

3	4

＜a＜2，

故a的取值范围是（

3	4

，2）．

故选D．