问题
填空题
函数f（x）=|x2-2x|-a有四个零点，则实数a的取值范围是 ______．
答案
令f（x）=|x2-2x|-a=0，
得a=|x2-2x|，
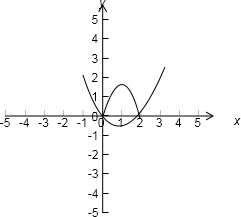
作出y=|x2-2x|与y=a的图象，
要使函数f（x）=|x2-2x|-a有四个零点，
则y=|x2-2x|与y=a的图象有四个不同的交点，
所以0＜a＜1，
故答案为：（0，1）．
搜题请搜索小程序“爱下问搜题”
函数f（x）=|x2-2x|-a有四个零点，则实数a的取值范围是 ______．
令f（x）=|x2-2x|-a=0，
得a=|x2-2x|，
作出y=|x2-2x|与y=a的图象，
要使函数f（x）=|x2-2x|-a有四个零点，
则y=|x2-2x|与y=a的图象有四个不同的交点，
所以0＜a＜1，
故答案为：（0，1）．