问题
选择题
f（x）=|x-2|-
|
答案
∵f（x）=|x-2|-
，求其零点，log x2
∴f（x）=0，
可得|x-2|=
，令g（x）=|x-2|，h（x）=log x2
，g（x）与h（x）图象有交点，如下图log x2
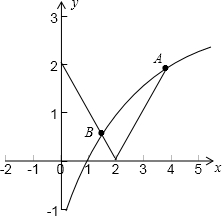
可知g（x）与h（x）交与两点A，B，
说明f（x）=|x-2|-
在定义域内的零点个数为2，log x2
故选B．
搜题请搜索小程序“爱下问搜题”
f（x）=|x-2|-
|
∵f（x）=|x-2|-
，求其零点，log x2
∴f（x）=0，
可得|x-2|=
，令g（x）=|x-2|，h（x）=log x2
，g（x）与h（x）图象有交点，如下图log x2
可知g（x）与h（x）交与两点A，B，
说明f（x）=|x-2|-
在定义域内的零点个数为2，log x2
故选B．