解∵设函数f（x）=x³+3x²-a，求导函数得f'（x）=3x²+6x

∴f'（x）=0的两根分别为x₁=-2，x₂=0

∵x＜-2或x＞0时，f'（x）＞0；-2＜x＜0时，f'（x）＜0

∴函数f（x）的减区间为（-2，0）；增区间为（-∞，-2）和（0，+∞）

因此，函数f（x）的极大值是f（-2）=4-a，极小值是f（0）=-a

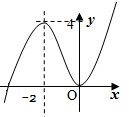
作出函数的草图，如右图所示，可得

（1）当4-a＜0或-a＞0时，即a＜0或a＞4时，函数f（x）的图象与x轴只有一个交点，

可得原方程只有一个根．

（2）当4-a=0或-a=0时，即a=0或a=4时，函数f（x）的图象与x轴有两个交点，即原方程有两个相异实根．

（3）当0＜a＜4时，函数f（x）的图象与x轴有三个交点，原方程有三个相异实根．