问题
选择题
设定义域为R的函数f(x)=
|
答案
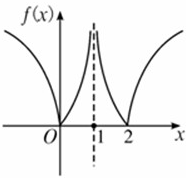
函数f(x)=
的图象,如图.|lg|x-1|| x≠1 0 x=1
由图知,f(x)图象关于x=1对称,且f(x)≥0,
若方程f2(x)+bf(x)+c=0 ①有7个解,
则方程t2+bt+c=0 ②有两个不等实根,且一根为正,一根为0.否则,
若方程②有两相等实根,则方程①至多有4个解,
若方程②有两个不等正实根,则方程①有8个解.
∵f(x)=0满足方程,则c=0,
又∵另一个f(x)>0,
∴b=-f(x)<0.
故b<0且c=0,
m=2010b∈(0,1),n=2010c=1;
所以m<n.
故选A.
