问题
计算题
(12分)一个不带电的金属板，表面有很薄的光滑绝缘层，与水平方向成θ角放置.金属板上B、C两点间的距离为L，在金属板上方的A点固定一个带电荷量为+Q的点电荷，金属板处在+Q的电场中.已知A、B、C三点在同一竖直平面内，且AB水平，AC竖直，如图所示.将一个带电荷量为+q(q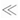 
Q，q对原电场无影响)可看做点电荷的小球，从B点无初速释放，如果小球质量为m，下滑过程中带电荷量不变，求：
(1)小球在B点的加速度；
(2)下滑到C点时的速度.
答案
(1)gsinθ (2)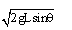 
(1)由于金属板处在点电荷Q形成的电场中达到静电平衡时，金属板表面是一个等势面，金属板表面处的电场线与金属板表面垂直，带电小球在沿金属板下滑的过程中，所受电场力与金属板表面垂直.则小球所受的合外力为F=mgsinθ，所以小球沿金属板表面做初速度为零的匀加速直线运动，故小球在B点的加速度为a=gsinθ. (6分) (2)根据运动学公式v2-v02=2ax可得： (2分) C点的速度为vC=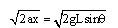 
(4分)或者根据机械能守恒得：mgLsinθ= 
mvC2
所以vC=