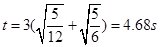问题
计算题
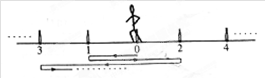
足球运动员常采用折返跑方式训练(如图所示),在直线跑道上每隔5m放一个空瓶,要求运动员以站立式起跑姿势站在起点“0”上,当听到“跑”的口令后,全力跑向“1”号瓶,推倒“1”号瓶后再全力跑向“2”号瓶,推倒“2”号瓶后……。运动员做变速运动时可看做匀变速直线运动,加速时加速度大小为4m/s2,减速时加速度大小为8m/s2,运动员推倒瓶子时速度为零。求运动员从开始起跑到推倒“2”号瓶所需的最短时间为多少?(运动员可看做质点,结果可以用根式表示)
答案
4.68s
题目分析: 设加速时加速度大小为a1,减速时加速度大小是a2,且a2=2a1。
运动员从0—1瓶加速时间为t1,减速时间为t1’;
运动员从1—2瓶加速时间为t2,减速时间为t2’;
如图可知道当位移一定时,每个过程只能是先匀加速后匀减速时间才最短,
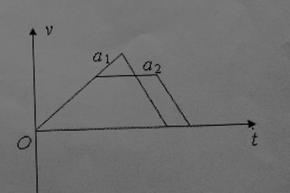
有:
速度关系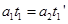
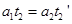
位移关系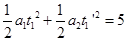
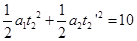
时间关系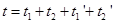
解得