问题
填空题
已知函数f(x)=|x|-2,若关于x的方程f2(x)-|f(x)|+k=0恰有8个不同的实数根,则实数k的取值范围是______.
答案
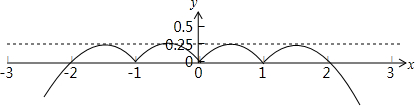
∵f(x)=|x|-2
∴方程f2(x)-|f(x)|+k=0,即(|x|-2)2-||x|-2|+k=0可化为
(x-2)2-(x-2)+k=0(x≥2)…①
或(x-2)2-(2-x)+k=0(0≤x<2)…②
或(x+1)2+(x+1)+k=0(-2<x<0)…③
或(x+1)2-(x+1)+k=0(x≤-2)…④
函数g(x)=-f2(x)+|f(x)|图象,如图所示,
由图象知实数k的取值范围为(0,
),1 4
故答案为(0,
).1 4
