问题
选择题
函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点，则实数b的取值范围是（ ）
|
答案
解：设y=f（x）=2x3+1，y=g（x）=3x2-b
∵y=2x3+1的图象与y=3x2-b的图象有三个不相同的交点，
∴方程f（x）=g（x）有三个不相等的实数根即：
2x3+1=3x2-b?b=-2x3+3x2-1 记F（x）=-2x3+3x2-1，得F′（x）=-6x（x-1），
列出下表：
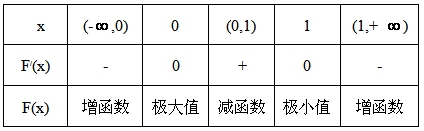
所以方程f（x）=g（x）有三个不相等的实数根的充要条件是函数F（x）的极大值大于b，
而极小值小于b
∴ 
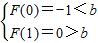?b∈（-1，0）
故选B