问题
选择题
设函数f(x)=lnx-
|
答案
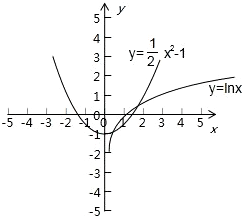
函数f(x)=lnx-
x2+1(x＞0)的零点，1 2
就是方程lnx-
x2+1=0(x＞0)的根，1 2
就是y=lnx， y=
x2-1(x＞0)图象的交点，1 2
如图：
函数y=f（x）在区间（0，1），（1，2）内均有零点．
故选A．
搜题请搜索小程序“爱下问搜题”
设函数f(x)=lnx-
|
函数f(x)=lnx-
x2+1(x＞0)的零点，1 2
就是方程lnx-
x2+1=0(x＞0)的根，1 2
就是y=lnx， y=
x2-1(x＞0)图象的交点，1 2
如图：
函数y=f（x）在区间（0，1），（1，2）内均有零点．
故选A．