问题
选择题
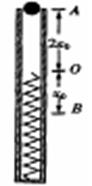
如图所示，在一直立的光滑管内放置一轻质弹簧，上端O点与管口A的距离为2xo，一质量为m的小球从管口由静止下落，将弹簧压缩至最低点B，压缩量为xo，不计空气阻力，则（ ）
A．弹簧的最大弹性势能为3mgx。
B．小球运动的最大速度等于2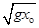
C．弹簧的劲度系数为mg/x。
D．小球运动中最大加速度为g
答案
答案：A
题目分析：小球从A点开始做自由落体运动，到O点时，由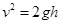
知：
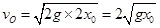，从O点开始压缩弹簧，由于开始时弹力小于重力，小球继续做加速运动，当弹力等于重力时，速度最大，然后做减速运动，故选项B错误；弹簧压缩量最大时弹性势能最大，所以由能量守恒定律可知：从A点到B点，小球减小的重力势能转化为弹性势能，即
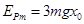，故选项A正确；由弹性势能的表达式
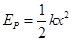可知：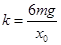
，故选项C错误；在B点，由牛顿第二定律可得：
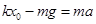，解得：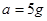
，故选项D错误．