问题
解答题
已知关于x的不等式|x-3|+|x-4|＜a，
(Ⅰ)当a=2时，解上述不等式；
(Ⅱ)如果关于x的不等式|x-3|+|x-4|＜a的解集为空集，求实数a的取值范围。
答案
解：(Ⅰ)原不等式|x-3|十|x-4|＜2，
当x＜3时，原不等式化为7-2x＜2，解得x＞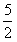
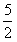，∴＜x＜3；
当3≤x≤4时，原不等式化为1＜2，∴3≤x≤4；
当x＞4时，原小等式化为2x-7＜2，解得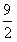x＜
，4＜x＜；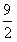
综上，原不等式解集为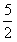{x|
＜x＜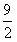
}。
(Ⅱ)作出y=|x-3|十|x-4|与y=a的图象，
若使|x-3|十|x -4|＜a解集为空集，
只须y=|x-3|+|x-4|图象在y=a的图象的上方，或y=a与y=1重合，
∴a≤l，
所以，a的取值范围为(-∞，1]。