解：∵当x∈[0，π]时，0＜f（x）＜1，f（x）为偶函数，

∴当x∈[-π，0]时，0＜f（x）＜1；

又∵f（x）的最小正周期为2π

∴当x∈[-2π，2π]时，0＜f（x）＜1；

∵x∈（0，π）且x≠时，（x- ）f′（x）＜0

∴当x∈（0，）时，f′（x）＞0，f（x）单调递增；当x∈（ ，π）时，f′（x）＜0，f（x）单调递减 y=f（x）与y=cosx的草图如下：

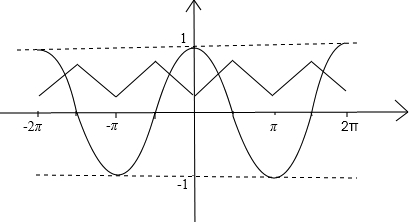
∴方程f（x）=cosx在[-2π，2π]上的又4个根

故选C