问题
选择题
| 考察下列函数: ①f(x)=sinx-x;②f(x)=|x2-3|-2;③f(x)=2x-x2;④f(x)=lnx-2cosx其中有三个零点的函数是( )
|
答案
解:∵sinx-x=0∴sinx=x
令y1=sinx,y2=x
根据这两个函数的图象在同一个坐标系中的位置关系知,两个图象有一个公共点坐标原点,
∴原函数的零点的个数是1,故①不正确
|x2-3|-2=0则|x2-3|=2结合图象可知有四个交点,故②不正确
2x-x2=0即2x=x2结合图象可知有3个交点,有两正根2和4和一负根
lnx-2cosx=0即lnx=2cosx,结合图象可知有3个交点

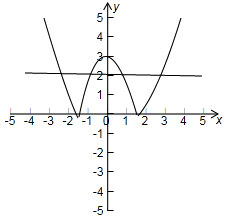
故选C.
