问题
解答题
(选作题)
设函数f(x)=|x-1|+|x-2|,
(1)画出函数y=f(x)的图像;
(2)若不等式|a+b|+|a-b| ≥|a|f(x)(a≠0,a、b∈R)恒成立,求实数x的范围。
答案
解:(1) ,
,
图像如下,
 ;
;
(2)由|a+b|+|a-b|≥|a|f(x),得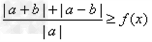 ,
,
又因为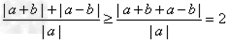 ,
,
则有2≥f(x),
解不等式2≥|x-1|+|x-2|,得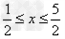 。
。
(选作题)
设函数f(x)=|x-1|+|x-2|,
(1)画出函数y=f(x)的图像;
(2)若不等式|a+b|+|a-b| ≥|a|f(x)(a≠0,a、b∈R)恒成立,求实数x的范围。
解:(1) ,
,
图像如下,
 ;
;
(2)由|a+b|+|a-b|≥|a|f(x),得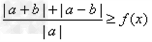 ,
,
又因为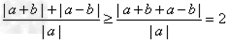 ,
,
则有2≥f(x),
解不等式2≥|x-1|+|x-2|,得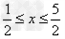 。
。