问题
解答题
设函数f(x)=2|x-l|+|x+2|,
(Ⅰ)求不等式f(x)≥4的解集;
(Ⅱ)若不等式f(x)<|m-2|的解集是非空的集合,求实数m的取值范围。
答案
解:(Ⅰ)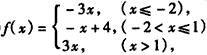 ,
,
令-x+4=4或3x=4,得x=0或x=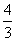 ,
,
所以不等式f(x)≥4的解集是{x|x≤0或x≥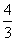 }。
}。
(Ⅱ)f(x)在(-∞,1]上递减,在[1,+∞)上递增,
所以f(x)≥f(1)=3,
由于不等式f(x)<|m-2|的解集是非空的集合,
所以|m-2|>3,解得m<-1或m>5,
即实数m的取值范围是(-∞,-1)∪(5,+∞)。
