解：（1）不等式|a+b|+|a-b|≥M·|a|恒成立，

即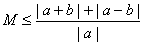对于任意的实数a（a≠0）和b恒成立，

只要M恒小于或等于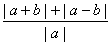的最小值，

因为 |a+b|+|a-b|≥ |（a+b）+（a-b）|=2|a|，

所以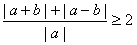

即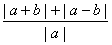的最小值是2，

所以M≤2，m=2。

（2）当x＜1时，原不等式化为-（x-1）-（x-2）≤2，

解得，

所以x的取值范围是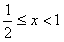

当1≤x≤2时，原不等式化为（x-1）-（x-2）≤2，

得x的取值范围是1≤x≤2

当x>2时，原不等式化为（x-1）+（x-2）≤2，

解得，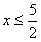

所以x的取值范围是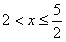

综上所述x的取值范围是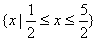。