问题
解答题
对于任意实数a(a≠0)和b,不等式|a+b|+|a-2b|≥|a|(|x-1|+|x-2|)恒成立,试求实数x的取值范围。
答案
解:原式等价于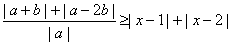
设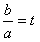
则原式变为|t+1|+|2t-1|≥|x-1|+|x-2|对任意t恒成立
因为|t+1|+|2t-1|=
最小值为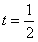 时取到,为
时取到,为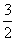
所以有
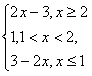
解得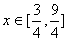 。
。
对于任意实数a(a≠0)和b,不等式|a+b|+|a-2b|≥|a|(|x-1|+|x-2|)恒成立,试求实数x的取值范围。
解:原式等价于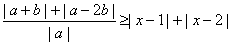
设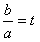
则原式变为|t+1|+|2t-1|≥|x-1|+|x-2|对任意t恒成立
因为|t+1|+|2t-1|=
最小值为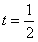 时取到,为
时取到,为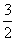
所以有
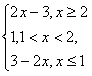
解得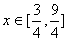 。
。