(15分)如图所示,相距L=0.4m、电阻不计的两平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连,导轨处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直于导轨平面。质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直。t=0时起棒在水平外力F作用下以初速度v0=2m/s、加速度a=1m/s2沿导轨向右匀加速运动。求:
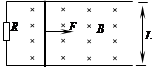
⑴t=1s时回路中的电流;
⑵t=1s时外力F大小;
⑶第1s内通过棒的电荷量。
⑴I=3A;⑵F=0.7N;⑶q=2.5C
题目分析:⑴t=1s时,棒的速度为:v1=v0+at=3m/s
此时由于棒运动切割产生的电动势为:E=BLv1=0.6V
根据闭合电路欧姆定律可知,此时回路中的感应电流为:I=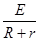 =3A
=3A
⑵对棒,根据牛顿第二定律有:F-ILB=ma
解得t=1s时外力F大小为:F=ILB+ma=0.7N
⑶在t=1s时间内,棒的位移为:x=v0t+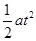
根据法拉第电磁感应定律可知,在这段时间内,棒切割平均感应电动势为: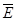 =
=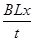
根据闭合电路欧姆定律可知,在这段时间内,回路中的平均感应电流为: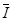 =
=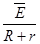
在第1s时间内,通过棒的电荷量为:q=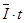
联立以上各式解得:q=2.5C
