问题
解答题
（Ⅰ）解不等式：|2x﹣1|﹣|x|＜1；
（Ⅱ）设f（x）=x2﹣x+1，实数a满足|x﹣a|＜1，求证：|f（x）﹣f（a）|＜2（|a|+1）．
答案
解：（Ⅰ）当x＜0时，原不等式可化为﹣2x+x＜0，解得x＞0，
又∵x＜0，∴x不存在．
当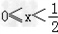
时，原不等式可化为﹣2x﹣x＜0，解得x＞0，
又∵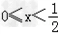
，∴
．
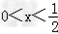当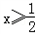
时，原不等式可化为2x﹣1﹣x＜1，解得x＜2，
又∵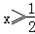
，∴
．
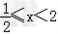综上，原不等式的解集为{x|0＜x＜2}．
（Ⅱ）∵f（x）=x2﹣x+1，实数a满足|x﹣a|＜1，
故|f（x）﹣f（a）|=|x2﹣x﹣a2+a|=|x﹣a||x+a﹣1|＜|x+a﹣1|
=|x﹣a+2a﹣1|≤|x﹣a|+|2a﹣1|＜1+|2a|+1=2（|a|+1）．
∴|f（x）﹣f（a）|＜2（|a|+1）．