问题
解答题
已知函数f（x）=|x+1|，g（x）=2|x|+a，
（Ⅰ）当a=0时，解不等式f（x）≥g（x）；
（Ⅱ）若存在x∈R，使得f（x）≥g（x）成立，求实数a的取值范围。
答案
解：（Ⅰ）|x+1|≥2|x|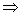
x2+2x+1≥4x2
，
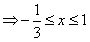∴解集为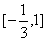
；
（Ⅱ）存在x∈R使|x+1|≥2|x|+a，
∴存在x∈R使|x+1|-2|x|≥a，
令φ（x）=|x+1|-2|x|，a≤φ（x）max，
，
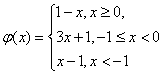当x≥0时，y≥1；-1≤x＜0时，-2≤y＜1；x＜-1时，y＜-2；
综上可得φ（x）≤1，
∴a≤1。
