问题
解答题
（选做题）已知函数f（x）=|2x-a|+a，
（1）若不等式f（x）≤6的解集为{x|-2≤x≤3}，求实数a的值；
（2）在（1）的条件下，若存在实数n使f（n）≤m-f（-n）成立，求实数m的取值范围。
答案
解：（1）由
得
，
∴
，
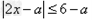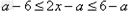即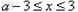
，
∴
，
∴
。
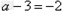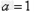（2）由（1）知
，
令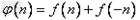
，
则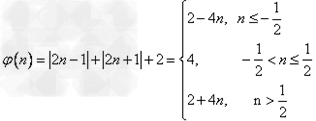
，
∴
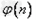的最小值为4，
故实数m的取值范围是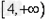
。
搜题请搜索小程序“爱下问搜题”
（选做题）已知函数f（x）=|2x-a|+a，
（1）若不等式f（x）≤6的解集为{x|-2≤x≤3}，求实数a的值；
（2）在（1）的条件下，若存在实数n使f（n）≤m-f（-n）成立，求实数m的取值范围。
解：（1）由得，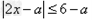
∴，
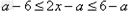即，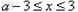
∴，
∴。
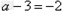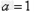（2）由（1）知，
令，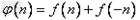
则，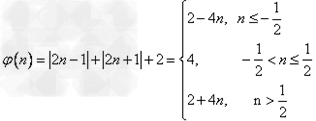
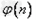∴的最小值为4，
故实数m的取值范围是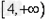。