解：（Ⅰ）不等式f（x）＞5 即|x﹣1|+|2x+2|＞5，

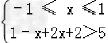∴①，或②，或③．

解①得 x＜﹣2，解②得 x∈，解③得 x＞．

故原不等式的解集为 {x|x＜﹣2，或 x＞ }．

（Ⅱ）由于函数f（x）=|x﹣1|+|2x+2|表示数轴上的x对应点到1对应点的距离加上 数轴上的x对应点到﹣1对应点的距离的2倍，

故当x=﹣1时，函数f（x）=|x﹣1|+|2x+2|有最小值等于2，即 f（x）∈[2，+∞）．

由于f（x）＜a（a∈R）的解集为空集，则a∈（﹣∞，2]．