问题
解答题
已知函数f（x）=|2x+1|，g（x）=|x|+a
（Ⅰ）当a=0时，解不等式f（x）≥g（x）；
（Ⅱ）若存在x∈R，使得f（x）≤g（x）成立，求实数a的取值范围．
答案
解：（Ⅰ）当a=0时，由f（x）≥g（x）得|2x+1|≥|x|，
两边平方整理得3x2+4x+1≥0，解得x≤﹣1或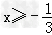
，
∴原不等式的解集为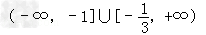
（Ⅱ）由f（x）≤g（x）得a≥|2x+1|﹣|x|，
令h（x）=|2x+1|﹣|x|，则 h（x）=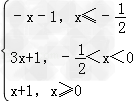
故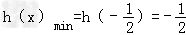
，从而所求实数a的范围为