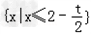问题
解答题
已知函数f（x）=|x﹣a|．
（I）若不等式f（x）≤m的解集为{x|﹣1≤x≤5}，求实数a，m的值．
（II）当a=2时，解关于x的不等式f（x）+t≥f（x+2t）（t≥0）．
答案
解：（Ⅰ）由|x﹣a|≤m得a﹣m≤x≤a+m，
所以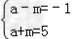
解之得
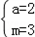为所求．
（Ⅱ）当a=2时，f（x）=|x﹣2|，
所以f（x）+t≧f（x+2t）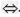
|x﹣2+2t|﹣|x﹣2|≤t，
①当t=0时，不等式①恒成立，即x∈R；
当t＞0时，不等式①
解之得x＜2﹣2t或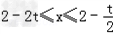
或x∈?，即
；
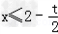综上，当t=0时，原不等式的解集为R，
当t＞0时，原不等式的解集为