问题
解答题
已知函数f(x)=|x-2|-|x+1| .
(Ⅰ)若f(x) ≤a 恒成立,求a 的取值范围;
(Ⅱ)解不等式f(x) ≥x2-2x.
答案
解:(1)
又当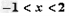
 时,
时,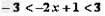 ,
,
∴
∴若使f(x)≤a恒成立,应有a≥fmax(x),即a≥3
∴a的取值范围是:[3,+∞)
(2)当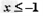 时,
时,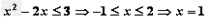 ;
;
当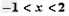 时,
时,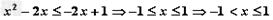 ;
;
当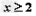 时,
时,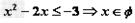
综合上述,不等式的解集为: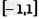
已知函数f(x)=|x-2|-|x+1| .
(Ⅰ)若f(x) ≤a 恒成立,求a 的取值范围;
(Ⅱ)解不等式f(x) ≥x2-2x.
解:(1)
又当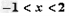
 时,
时,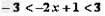 ,
,
∴
∴若使f(x)≤a恒成立,应有a≥fmax(x),即a≥3
∴a的取值范围是:[3,+∞)
(2)当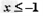 时,
时,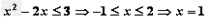 ;
;
当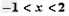 时,
时,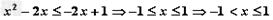 ;
;
当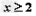 时,
时,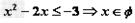
综合上述,不等式的解集为: