问题
解答题
已知关于x的不等式|x-3|+|x-4|<a.
(1)当a=2时,解上述不等式;
(2)如果关于x的不等式|x-3|+|x-4|<a的解集为空集,求实数a的取值范围.
答案
(1)原不等式|x-3|+|x-4|<2
当x<3时,原不等式化为7-2x<2,解得x>
,∴5 2
<x<35 2
当3≤x≤4时,原不等式化为1<2,∴3≤x≤4
当x>4时,原不等式化为2x-7<2,解得x<
,∴4<x<9 2 9 2
综上,原不等式解集为{x|
<x<5 2
};(5分)9 2
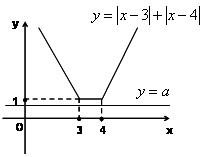
(2)法一、作出y=|x-3|+|x-4|与y=a的图象,
若使|x-3|+|x-4|<a解集为空集只须y=|x-3|+|x-4|图象在y=a的图象的上方,
或y=a与y=1重合,∴a≤1
所以,a的范围为(-∞,1],(10分)
法二、:y=|x-3|+|x-4|=2x-7 x≥4 1 3≤x≤4 7-2x x<3
当x≥4时,y≥1
当3≤x<4时,y=1
当x<3时,y>1
综上y≥1,原问题等价为a≤[|x-3|+|x-4|]min
∴a≤1(10分)
法三、:∵|x-3|+|x-4|≥|x-3-x+4|=1,
当且仅当(x-3)(x-4)≤0时,上式取等号
∴a≤1.
