问题
解答题
(选做题)已知f(x)=|x+1|+|x﹣1|,不等式f(x)<4的解集为M.
(1)求M;
(2)当a,b∈M时,证明:2|a+b|<|4+ab|.
答案
(Ⅰ)解:f(x)=|x+1|+|x﹣1|= 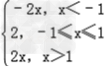
当x<﹣1时,由﹣2x<4,得﹣2<x<﹣1;
当﹣1≤x≤1时,f(x)=2<4;
当x>1时,由2x<4,得1<x<2.
所以M=(﹣2,2).
(Ⅱ)证明:当a,b∈M,即﹣2<a,b<2,
∵4(a+b)2﹣(4+ab)2=4(a2+2ab+b2)﹣(16+8ab+a2b2)=(a2﹣4)(4﹣b2)<0,
∴4(a+b)2<(4+ab)2,
∴2|a+b|<|4+ab|.
