问题
解答题
(选做题)
已知函数f(x)=|x﹣a|.不等式f(x)≤3的解集为{x|﹣1≤x≤5}.
(1)求实数a的值;
(2)若f(x)+f(x+5)≥c2﹣4c对一切实数x恒成立,求实数c的取值范围.
答案
解:(1)∵f(x)≤3即|x﹣a|≤3,得a﹣3≤x≤a+3.
∴f(x)≤3的解集是[a﹣3,a+3],
结合题意,得 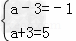 ,
,
可得a=2.
(2)∵f(x)=|x﹣2|,
∴原不等式即:|x﹣2|+|x+3|≥c2﹣4c对一切实数x恒成立,
∵|x﹣2|+|x+3|≥|(x﹣2)﹣(x+3)|=5,即|x﹣2|+|x+3|的最小值为5
∴5≥c2﹣4c,即c2﹣4c﹣5≤0,
解之得﹣1≤c≤5
