问题
解答题
选做题
设函数f(x)=|x-a|+3x,其中a>0。
(Ⅰ)当a=1时,求不等式f(x)≥3x+2的解集;
(Ⅱ)若不等式f(x)≤0的解集为{x|x≤-1},求a的值。
答案
解:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x-1|≥2。
由此可得 x≥3或x≤-1。
故不等式f(x)≥3x+2的解集为{x|x≥3或x≤-1}。
( Ⅱ) 由f(x)≤0 得 |x-a|+3x≤0
此不等式化为不等式组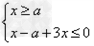 或
或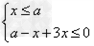
即 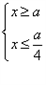 或
或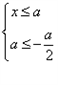
因为a>0,所以不等式组的解集为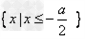
由题设可得 = -1,故a=2
= -1,故a=2
