问题
计算题
(16分)如图所示，光滑水平面上有一木板，质量M＝1.0kg，长度L＝1.0m．在木板的最左端有一个小铁块(可视为质点)，质量m＝1.0kg．小铁块与木板之间的动摩擦因数μ＝0.30．开始时它们都处于静止状态，某时刻起对木板施加一个水平向左的拉力F，g取10m/s2．求：
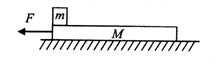
⑴拉力F至少多大能将木板抽出；
⑵若F＝8N将木板抽出，则抽出过程中摩擦力分别对木板和铁块做的功．
答案
⑴F＞6N；⑵W2＝－7.5J，W1＝4.5J
题目分析：⑴当小铁块与木板之间存在相对运动时，设小铁块运动的加速度为a1，木板运动的加速度为a2，根据牛顿第二定律有：μmg＝ma1，F－μmg＝Ma2
要使木板能从小铁块下方抽出，需满足a2＞a1
联立以上两式解得：F＞μ(M＋m)g＝6N
⑵由可知，当F＝8N将木板从小铁块下方抽出，小铁块运动的加速度为：a1＝μg＝3m/s2
木板运动的加速度为：a2＝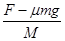
＝5m/s2
设抽出过程的时间为t，根据匀变速直线运动规律和空间几何关系有：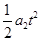
－
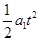＝L
解得：t＝1s
所以小铁块运动的位移为：x1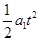＝＝1.5m
木板运动的位移为：x2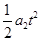＝＝2.5m
根据功的定义式可知，摩擦力对小铁块做的功为：W1＝μmgx1＝4.5J
摩擦力对木板做的功为：W2＝－μmgx2＝－7.5J