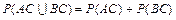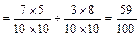问题
解答题
有外形相同的球分装三个盒子，每盒10个，其中，第一个盒子中7个球标有字母A，3个球标有字母B；第二个盒子中有红球和白球各5个；第三个盒子中则有红球8个，白球2个.试验按如下规则进行：先在第一个盒子中任取一球，若取得标有字母A的球，则在第二个盒子中任取一球；若第一次取得标有字母B的球，则在第三个盒子中任取一球.若第二次取出的是红球，则称试验成功.求试验成功的概率.
答案
解：<法一>
设A={从第一个盒子中取得标有字母A的球}，B={从第一个盒子中取得标有字母B的球}，C={第二次取出的是红球}，
则试验成功可表示为“AC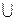
BC”,又事件“AC”与事件“BC”互斥，所以
P(AC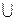BC)=P(AC)+P(BC)=P(C|A)P(A)+P(C|B)P(B)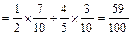
<法二>
