问题
选择题
定义在R上的函数f(x)=
|
答案
对于f2(x)+bf(x)+c=0来说,f(x)最多只有2解,又f(x)=
(x≠2),当x不等于2时,x最多四解.1 |x-2|
而题目要求5解,即可推断f(2)为一解!
假设f(x)的1解为A,得f(x)=
=A;1 |x-2|
算出x1=2+A,x2=2-A,x1+x2=4;
同理:x3+x4=4;
所以:x1+x2+x3+x4+x5=4+4+2=10;
f(x1+x2+x3+x4+x5)=
.1 8
故选B.

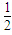 mgtgθ
mgtgθ mgsinθ
mgsinθ