问题
解答题
设函数f(x)=lnx-
(1)当a=2时,求f(x)的最大值; (2)令F(x)=f(x)+
(3)当a=0时,方程mf(x)=x2有唯一实数解,求正数m的值. |
答案
解(1)a=2时,f(x)=lnx+x-x2,f/(x)=
+1-2x…(1分),1 x
解f′(x)=0得x=1或x=-
(舍去)…(2分),1 2
当x∈(0,1)时,f′(x)>0,f(x)单调增加,
当x∈(1,+∞)时,f′(x)<0,f(x)单调减少…(3分),
所以f(x)的最大值为f(1)=0…(4分)
(2)F(x)=lnx+
(0<x≤3),k=F/(x0)=a x
-1 x0
(0<x0≤3)…(6分)a x02
由k≤
恒成立得a≥x0-1 2
x02=-1 2
(x0-1)2+1 2
恒成立…(7分)1 2
因为-
(x0-1)2+1 2
≤1 2
,等号当且仅当x0=1时成立…(8分),1 2
所以a≥
…(9分)1 2
(3)a=0时,方程mf(x)=x2即x2-mx-mlnx=0,
设g(x)=x2-mx-mlnx,
解g/(x)=2x-m-
=0…(10分),得x1=m x
(<0舍去),x2=m- m2+8m 4
,m+ m2+8m 4
类似(1)的讨论知,g(x)在x∈(0,x2)单调增加,
在x∈(x2,+∞)单调减少,最大值为g(x2)…(11分),
因为mf(x)=x2有唯一实数解,g(x)有唯一零点,所以g(x2)=0…(12分),
由
得x2+2lnx2-1=0,g′ (x2)=0 g(x2)=0
因为h(x)=x+lnx-1单调递增,且h(1)=0,
所以x2=1…(13分),
从而m=1…(14分).

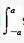 sinx?[f(x)+f(-x)]dx等于:()
sinx?[f(x)+f(-x)]dx等于:()