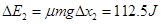问题
计算题
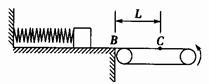
如图所示，质量为m＝1 kg的滑块，放在光滑的水平平台上，平台的右端B与足够长的水平传送带相接，皮带轮的半径为R＝0.5m，且以角速度ω＝12 rad／s逆时针转动（传送带不打滑），先将滑块缓慢向左压缩固定在平台上的轻弹簧，然后突然释放，当滑块滑到传送带上距B端L=15m的C点时，与传送带速度大小相等，滑块与传送带之间的动摩擦因数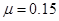
。（g="10" m/s2）求：
（1）释放滑块前弹簧具有的弹性势能；
（2）滑块从B到C所用的时间；
（3） 滑块从B到C系统因摩擦增加的内能。
答案
（1）
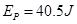
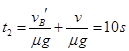
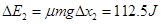
题目分析：（1）传送带的速度：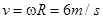
，vmax和vmin
若一直减速：由动能定理可得：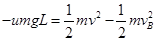
可求得：
。
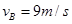由能量守恒定律可得：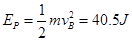
.
若先减速到零再反向加速到C点与传送带速度大小相等，由运动学公式可得：
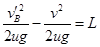，解得：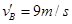
由能量守恒定律可得：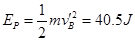
（2）若一直减速，设由B到C的运动时间为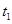
则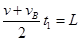
得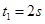
若先减速到零再反向加速到Ｃ点，设由Ｂ到Ｃ的运动时间为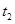
则：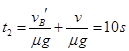
（３）若一直减速到Ｃ与带速度大小相等，相对位移的大小
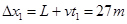
系统产生的内能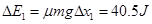
若先减速到零再反向加速到Ｃ点, 相对位移的大小
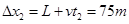
系统产生的内能