问题
解答题
一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分.
(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率;
(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分ξ的概率分布列及数学期望.
答案
(Ⅰ)由题意知本题是一个等可能事件的概率,
试验发生包含的事件数C53,
设“一次取出3个球得4分”的事件记为A,
它表示取出的球中有1个红球和2个黑球的情况,
满足条件的事件数C21C32
则P(A)=
=C 12 C 23 C 35 3 5
(Ⅱ)由题意,ξ的可能取值为3.4.5.6.因为是有放回地取球,
所以每次取到红球的概率为
,取到黑球的概率为2 5
.3 5
P(ξ=3)=
(C 33
)3=3 5 27 125
P(ξ=4)=
(C 23
)2?3 5
=2 5 54 125
P(ξ=5)=
(C 13
)?(3 5
)2=2 5 36 125
P(ξ=6)=
(C 03
)3=2 5 8 125
∴ξ的分布列为
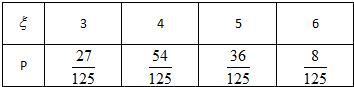
数学期望:Eξ=3×
+4×27 125
+5×54 125
+6×36 125
=8 125 21 5
