假定某存货的年需要量为1440件,经济批量订货次数为每年10次,单位储存变动成本为25元,单位缺货成本为20元,交货时间为25天。已知交货期内的存货需要量及其概率分布为:
| 需要量(25×d) | 25 | 50 | 75 | 100 | 125 | 150 | 175 |
| 概率(Pi) | 0.05 | 0.10 | 0.15 | 0.25 | 0.20 | 0.15 | 0.10 |
要求:
计算该存货的最佳再订货点,并进行保险储备量决策。
参考答案:
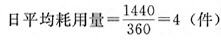
不设保险储备量时的再订货点为=Ld=25×4=100(件)
计算不同保险储备量的总成本:
(1)不设保险储备量(B=0),以100件为再订货点。
缺货量S0=(125-100)×0.2+(150-100)×0.15+(175-100)×0.10
=20(件)
总成本TC(S、B)=20×20×10+0×25=4000(元)
(2)设保险储备量为25件(B=25),以125为再订货点。
缺货量S25=(150-125)×0.15+(175-125)×0.10=8.75(件)
总成本TC(S、B)=20×8.75×10+25×25=2375(元)
(3)设保险储备量为50件(B=50),以150为再订货点。
缺货量S50=(175-150)×0.1=2.5(件)
总成本TC(S、B)=20×2.5×10+50×25=1750(元)
(4)设保险储备量为75件(B=75),以175为再订货点。
缺货量S75=0
总成本TC(S、B)=20×0×10+75×25=1875(元)
当B=50件,总成本为1750元,是各总成本中最低的。故应确定保险储备量为50件,或者说应确定以150件为再订货点。
