问题
问答题
设A是三阶可逆矩阵，α=[a1，a2，a3]T，β=[b1，b2，b3]T是3维列向量，且βlArα≠-1．
(Ⅰ)验证：
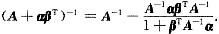
(Ⅱ)设
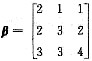，利用(Ⅰ)求β-1．
答案
参考答案：(Ⅰ)
[*]
故 [*]
(Ⅱ)[*]
其中 α=[1，2，3]T， β=[1，1，1]T，
故 B-1=(E+αβT)-1
[*]
[*]
搜题请搜索小程序“爱下问搜题”
设A是三阶可逆矩阵，α=[a1，a2，a3]T，β=[b1，b2，b3]T是3维列向量，且βlArα≠-1．
(Ⅰ)验证：
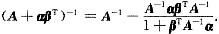
(Ⅱ)设
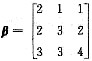，利用(Ⅰ)求β-1．
参考答案：(Ⅰ)
[*]
故 [*]
(Ⅱ)[*]
其中 α=[1，2，3]T， β=[1，1，1]T，
故 B-1=(E+αβT)-1
[*]
[*]