问题
问答题
已知随机变量X的概率密度为
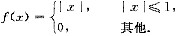
求Y=X2+1的概率密度fY(y).
答案
参考答案:FY(y)=P(Y≤y)=P(X2+1≤y)=P(X2≤y-1).
当1≤y≤2时,FY(y)=P(X2≤y-1)=P(|X|≤[*])
[*]
=y-1:
当y>2时,FY(y)=P(X2≤y-1)=1;
当y<1时,FY(y)=0.
所以[*]即Y服从[1,2]上的均匀分布.
解析:
[分析]: f(x)是偶函数,利用此性质可简化计算.
Y=X2+1,所以fY(y)在(-∞,1)范围内必为零.
