问题
问答题
设x＞0，证明
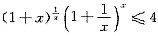，且仅在x=1处等号成立．
答案
参考答案：先证明当0＜x＜1时，[*]，命
[*]
有 F(1)=0，
[*]
记[*]，有ψ(0)=0，[*]，从而知，当0＜x＜1时，ψ(0)＜0，即有F"(x)＜0.因F’(1)=0，所以当0＜x＜1时F’(x)＞0.又因F(1)=0，所以当0＜x＜1时F(x)＜0，从而知当0＜x＜1时
[*]
上式中命[*]，故知当1＜u＜+∞时，[*]，又当x=1时[*]．所以当0＜x＜+∞时，有[*]，且仅当x=1时等号才成立．