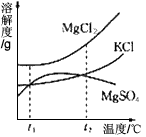
问题
解答题
附加题选做题D.(选修4-5:不等式选讲)
设函数f(x)=|x-1|+|x+1|,若不等式|a+b|-|2a-b|≤|a|•f(x)对任意a,b∈R且a≠0恒成立,求实数x的范围.
答案
由f(x)≥
,对任意的a,b∈R,且a≠0恒成立,|a+b|-|2a-b| |a|
而
≤|a+b|-|2a-b| |a|
=3,|a+b+2a-b| |a|
∴f(x)≥3,即|x-1|+|x+1|≥3,
解得x≤-
,或x≥3 2
,3 2
所以x的范围为{x|x≤-
,或x≥3 2
}. …(10分)3 2