问题
解答题
已知函数f(x)=lnx+cosx(x∈[π,2π]).
(1)判断函数f(x)的单调性,并求函数f(x)的值域;
(2)证明方程f(x)=x-π在[π,2π]上必有一根.
答案
(1)[π,2π]内,f1(x)=lnx是增函数,f2(x)=cosx也是增函数,…(2分)
∴f(x)=lnx+cosx在[π,2π]内是增函数.…(3分)
∴fmin(x)=f(π)=lnπ-1=ln
,fmax(x)=f(2π)=ln2π+1=ln2πe,…(5分)π e
∴函数f(x)的值域是[ln
,ln2πe].…(6分)π e
(2)设g(x)=f(x)-x+π=lnx+cosx-x+π,…(8分)
由g(π)=lnπ-1>lne-1=0,g(2π)=ln2π+1-π<lne2+1-π=3-π<0,…(12分)
∵g(π)•g(2π)<0,…(13分)
∴方程f(x)=x-π在[π,2π]必有一根.…(14分)

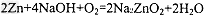 ,下列有关锌--空气电池说法正确的是[ ]
,下列有关锌--空气电池说法正确的是[ ]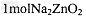 转移4mol电子
转移4mol电子