问题
解答题
一个口袋中装有标号为1,2,3的6个小球,其中标号1的小球有1个,标号2的小球有2个,标号3的小球有3个,现在口袋中随机摸出2个小球.
(Ⅰ)求摸出2个小球标号之和为3的概率;
(Ⅱ)求摸出2个小球标号之和为偶数的概率;
(Ⅲ)用X表示摸出2个小球的标号之和,写出X的分布列,并求X的数学期望E(X).
答案
(I)设“摸出2个小球标号之和为3”为事件A,
则P(A)=
=C 12 C 26 2 15
所以摸出2个小球标号之和为3的概率为
.2 15
(II)设“摸出2个小球标号之和为偶数”为事件B,
摸出2个小球标号之和为偶数有3中可能(1,3),(2,2),(3,3),
其中摸出2个小球标号为(1,3)的概率为
=C 13 C 26 1 5
摸出2个小球标号为(2,2)的概率为
=C 22 C 26
,1 15
摸出2个小球标号为(3,3)的概率为
=C 23 C 26
.1 5
所以摸出2个小球标号之和为偶数的概率为
+1 5
+1 15
=1 5 7 15
(III)依题意X的可能取值为3,4,5,6
P(X=3)=
; P(X=3)=2 15
=
+C 13 C 22 C 26 4 15
P(X=5)=
=C 13 C 12 C 26
;P(X=6)=2 5
=C 23 C 26 1 5
所以X的分布列为
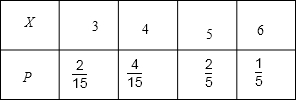
从而E(X)=3×
+4×2 15
+5×4 15
+6×2 5
=1 5
.14 3
