问题
填空题
关于x的方程
|
答案
原方程的解可以视为函数y=x-a(y≥0)与函数y=
的图象的交点的横坐标.1-x2
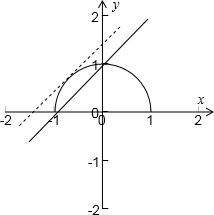
函数y=
的图象是半圆y2=1-x2(y≥0),如图所示,1-x2
当直线与圆相切时,
=1,∴a=-|a| 2
(正值舍去)2
利用平行直线系y=x-a(y≥0)与函数y=
的图象有两个不同的交点,可得实数a的取值范围是(-1-x2
,-1]2
故答案为:(-
,-1]2
关于x的方程
|
原方程的解可以视为函数y=x-a(y≥0)与函数y=
的图象的交点的横坐标.1-x2
函数y=
的图象是半圆y2=1-x2(y≥0),如图所示,1-x2
当直线与圆相切时,
=1,∴a=-|a| 2
(正值舍去)2
利用平行直线系y=x-a(y≥0)与函数y=
的图象有两个不同的交点,可得实数a的取值范围是(-1-x2
,-1]2
故答案为:(-
,-1]2
