（20分）传送带以稳定的速度v=6m/s顺时针转动，传送带与水平面的夹角θ=37°，现在将一质量m=2kg的物体（可以看作质点）轻放在其底端，传送带顶端平台上的人通过轻绳以恒定的拉力F=20N拉物体，经过一段时间物体被拉到斜面顶端，如图所示，已知传送带底端与顶端的竖直高度H=6m，物体与传送带之间的动摩擦因数μ=0.25，设最大静摩擦力等于滑动摩擦力．
（g取10m/s2，sin 37°=0.6，cos37°=0.8）
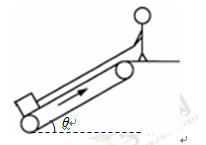
（1）从底端开始经多长时间物体与传送速度相同?
（2）若达到共速后保持拉力不变，物体还需多长时间到达斜面顶端？
（3）若物体与传送带达到速度相等的瞬间，突然撤去拉力，物体还需要多长时间离开传送带？(结果可用根式表示)
(1)1s (2)1s (3) 1.5+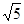
s
题目分析：解：(5分)（1） 物体在达到与传送带速度v=6m/s相等前，有：
F+μmgcos37°-mgsin37°=ma1 (2分)
解得a1=6m/s2
由v=a1t1，t1=1s (2分)
位移s1=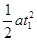
=3m (1分)
(2)(6分)达到共速后，有：F-μmgcos37°-mgsin37°=ma2 ( 2分)
解得a2=2m/s2，物体匀加速上滑
位移s2=10-3=7m (1分)
则s2= 
(2分)
解得t2=1s (1分)
（3）(9分)在物品与传送带达到同速瞬间撤去恒力F，
由于μmgcos37°=4N，mgsin37°=12N，
故mgsin37°＞μmgcos37°，则此后物体做匀减速运动，加速度大小为a3
mgsin37°-μmgcos37°=ma3
a3=" 4" m/s2 (2分)
设再过t3时间物体的速度减为零，则t3=1.5s (1分)
此过程物体通过的位移为x3=
=4.5m (2分)
由于传送带总长为10m，x1+x3＜10m，说明此后物体速度减速为零后沿传送带以a3加速下滑． (1分)
设下滑的时间为t4．则有
代入数据解得t4=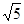 s (2分)
故撤去拉力，物体还需要时间t’=t3+t4=1.5+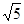s (1分)