问题
解答题
对任意实数a(a≠0)和b，不等式|a+b|+|a-b|≥|a|(|x-1|+|x-2|)恒成立，试求实数x的取值范围.
答案
所求的x的取值范围是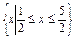
依题意，|x-1|+|x-2|≤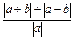
恒成立，
故|x-1|+|x-2|≤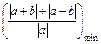
.
因为|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,
当且仅当(a+b)(a-b)≥0时取“=”，
所以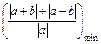=2.
所以x的取值范围即为不等式|x-1|+|x-2|≤2的解.
解上述不等式得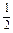
≤x≤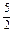
，
所以所求的x的取值范围是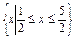.