问题
计算题
如图所示，ABC为绝缘体轨道，斜面部分倾角为30o，与下滑物体间动摩擦因数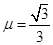
，水平轨道光滑。斜面轨道处于场强为E=l×106V/m、方向平行斜面向下的匀强电场中。小物体甲的质量m=0.1kg，带正电，电荷量为q=0.5×10-6 C，从斜面上高h="5" cm的A点由静止释放．同时小物体乙（不带电）自C点以速度v0沿水平面向左匀速运动，C点与斜面底端B处的距离L="0.4" m．甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去，甲释放后经过t="l" s刚好追上乙。取g=" 10" m/s2，求：
（1）甲沿斜面运动的加速度的大小：
（2）甲到达B点时的速率：
（3）乙的速度v0的大小。
答案
（1）5 m/s2 （2）
（3）0.4 m/s
题目分析：（1）以小球甲为研究对象，根据牛顿第二定律可得：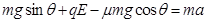
代入数据得：a="5" m/s2
（2）设甲在斜面上运动的时间为t1，运动到B处时的速度为v1
由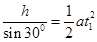
得：
所以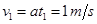
（3）从B处到追上小球乙所有时间为t2，则：
t2=t-t1=0.8s；v0t+L=v1t2
联立得：v0=0.4 m/s