问题
选择题
已知
|
答案
f（x）=0得：
+|x|-2=0，a2-x2
即：
=2-|x|，a2-x2
由题意可知：要研究函数f(x)=
+|x|-2的零点个数，只需研究函数y=a2-x2
，y=2-|x|的图象交点个数即可．a2-x2
画出函数y=
，y=2-|x|的图象，a2-x2
由图象可得有4个交点．
故选D．
搜题请搜索小程序“爱下问搜题”
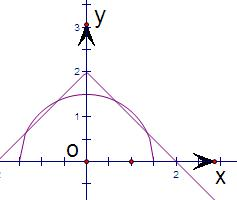
已知
|
f（x）=0得：
+|x|-2=0，a2-x2
即：
=2-|x|，a2-x2
由题意可知：要研究函数f(x)=
+|x|-2的零点个数，只需研究函数y=a2-x2
，y=2-|x|的图象交点个数即可．a2-x2
画出函数y=
，y=2-|x|的图象，a2-x2
由图象可得有4个交点．
故选D．